您现在的位置是：首页 > WEB开发 > 正文

WEB开发

Box-Jenkins时间序列预测模型

1987web2023-10-06WEB开发58

Itisalwaysverydifficulttopredictthefuture.Indeedithasbeenlikenedtodrivingacarblind

It is always very difficult to predict the future. Indeed it has been likened to driving a car blindfolded while following instructions given by a person looking out of the back window.

————Professor A.C.Harvey (Dept of Statistical and Mathematical Sciences, LSE)

最近正在复习统计预测模型，顺手抄下了各种模型的笔记（纯干货），需要的读者自行拿去，如无丝毫兴趣，请自行忽略。

统计学上常用公式：

c o v (X, Y) = E [(X - E (X)) (Y - E (Y))] = E [X Y] - E [X] E [Y]

cov(X,Y)=E[(X-E(X))(Y-E(Y))]=E[XY]-E[X]E[Y]

c o v (a + b X, c + d Y) = b d c o v (X, Y)

cov(a+bX,c+dY)=bdcov(X,Y)

c o v (X, X) = v a r (X)

cov(X,X)=var(X)

v a r (X + Y) = v a r (X) + v a r (Y) + 2 c o v (X, Y)

var(X+Y)=var(X)+var(Y)+2cov(X,Y)

c o r r (X, Y) = \frac{c o v (X, Y)}{\sqrt{v a r (X) v a r (Y)}}

corr(X,Y)=\frac{cov(X,Y)}{\sqrt{var(X)var(Y)} }

1. Stationary Processes.

i.Autoregressive process of order p. $A R (p)$ AR(p):

Y_{t} = ϕ_{1} Y_{t - 1} + ϕ_{2} Y_{t - 2} + . . . + ϕ_{p} Y_{t - p} + ϵ_{t} = Σ_{1}^{p} ϕ_{i} Y_{t - i} ϵ_{t} : W N (0, σ^{2})

Y_t=\phi_1Y_{t-1}+\phi_2Y_{t-2}+...+\phi_pY_{t-p}+\epsilon_t =\Sigma _1^p\phi_iY_{t-i}\\ \epsilon_t :WN(0,\sigma^2)

ii.Moving average process of order q. $M A (q)$ MA(q):

Y_{t} = ϵ_{t} - θ_{1} ϵ_{t - 1} - θ_{2} ϵ_{t - 2} - . . . - θ_{q} ϵ_{t - q} = ϵ_{t} - Σ_{i = 1}^{q} θ_{i} ϵ_{t - i} ϵ_{t} : W N (0, σ^{2})

Y_t=\epsilon_t-\theta_1\epsilon_{t-1}-\theta_2\epsilon_{t-2}-...-\theta_q\epsilon_{t-q} =\epsilon_t-\Sigma_{i=1}^{q}\theta_i\epsilon_{t-i}\\ \epsilon_t:WN(0,\sigma^2)

iii.Autoregressive,moving average process. $A R M A (p, q)$ ARMA(p,q):

Y_{t} = ϕ_{1} Y_{t - 1} + ϕ_{2} Y_{t - 2} + . . . + ϕ_{p} Y_{t - p} + ϵ_{t} - θ_{1} ϵ_{t - 1} - . . . - θ_{q} ϵ_{t - q} ϵ_{t} : W N (0, σ^{2})

Y_t=\phi_1Y_{t-1}+\phi_2Y_{t-2}+...+\phi_pY_{t-p}+\epsilon_t-\theta_1\epsilon_{t-1}-...-\theta_q\epsilon_{t-q}\\ \epsilon_t:WN(0,\sigma^2)

2.Non-stationary Processes.

i.Integrated autogressive moving average process of order(p,d,q). $A R I M A (p, d, q)$ ARIMA(p,d,q):

ϕ (B) (1 - B)^{d} Y_{t} = θ (B) ϵ_{t} B : B a c k s h i f t - o p e r a t o r - B^{d} Y_{t} = Y_{t - d}

\phi(B)(1-B)^dY_t=\theta(B)\epsilon_t \\ B:Backshift-operator -B^dY_t=Y_{t-d}

ii.Seasonal moving average process. $S M A (Q)_{s}$ SMA(Q)_s

Y_{t} = ϵ_{t} - Θ_{1} ϵ_{t - s} - Θ_{2} ϵ_{t - 2 s} - . . . - Θ_{t} ϵ_{t - Q s}

Y_t=\epsilon_t-\Theta_1\epsilon_{t-s}-\Theta_2\epsilon_{t-2s}-...-\Theta_t\epsilon_{t-Qs}

iii.Seasonal autogressive process. $S A R (P)_{s}$ SAR(P)_s

Y_{t} = Φ_{1} Y_{t - s} + Φ_{2} Y_{t - 2 s} + . . . + Φ_{P} Y_{t - P s} + ϵ_{t}

Y_t=\Phi_1Y_{t-s}+\Phi_2Y_{t-2s}+...+\Phi_PY_{t-Ps}+\epsilon_t

iv.Multiplicative seasonal autogresssive moving average process of order $(p, q) \times (P, Q)_{s}$ (p,q)\times (P,Q)_s. $S A R M A (p, q) \times (P, Q)_{s}$ SARMA(p,q)\times(P,Q)_s

ϕ (B) Φ (B) Y_{t} = θ (B) Θ (B) ϵ_{t}

\phi(B)\Phi(B)Y_t=\theta(B)\Theta(B)\epsilon_t

v.Integrated seasonal autoregressive moving average process of order $(p, d, q) \times (P, D, Q)_{s}$ (p,d,q)\times(P,D,Q)_s

ϕ (B) Φ (B) (1 - B)^{d} (1 - B^{s})^{D} = θ (B) Θ (B) ϵ_{t}

\phi(B)\Phi(B)(1-B)^d(1-B^s)^D=\theta(B)\Theta(B)\epsilon_t

现在许多做社会学科研究的都会用到一些统计方法，这些统计方法都有一个通用的前提是必须首先获取大量的时间序列数据，这个要求在今天这个大数据时代似乎并不是很难达到。就金融方面而言，在股票方面，人们可以轻松地从Google Finance 或者 Yahoo Finance 网站上获取相应的股票数据（国内的Wind资讯，国外的Bloomberg），其他方面的数据也可以从相应的管理统计部门获取。

而在获取了相应的时间序列数据以后，一般的研究方法都是统计建模，然后在此基础上做出合理的预测。就对时间序列的预测而言有很多模型及方法。许多学者也对模型的预测发表了自己的看法。其中应用比较广泛和实用的是Box-Jenkins理论。

Box-Jenkins理论框架：

第一步：根据数据估计模型，比如是MA,AR, ARMA, ARIMA,还是 SARMA等等；

第二步：估计模型中的参数， $ϕ$ \phi, $θ$ \theta, $Φ$ \Phi, $Θ$ \Theta等；

第三步：检查所得模型是否准确有效，如果比较准确，执行第四步，否则返回第一步；

第四步：预测。

暂时写这么多，有不准确的地方，还希望不吝赐教。

参考：

Chatfield,C., The analysis of time series, Chapman and Hall

Box,G & Jenkins, G, Time series analysis; forecasting and control, Holden Day

WEB开发

Box-Jenkins时间序列预测模型

浏览器访问

手把手带你玩转k8s-jenkins安装与流水线

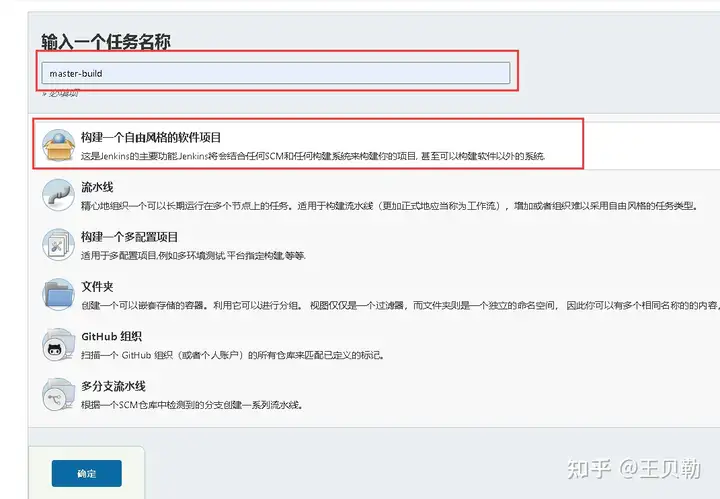
关于Jenkins的优点

相关文章